数列an的前n项和为sn,a1=1,an+1=2sn-前沿资讯
时间：2023-03-09 01:07:59 来源：关注网
(相关资料图)
1、已知正项数列{an}的前n项和为Sn,根号Sn是4分之1与（an+1）的等比中项.（1）求证数列｛an｝是等比数列. 由已知正项数列{an}的前n项和为Sn,根号Sn是4分之1与（an+1）的等比中项. 得Sn是4分之1与（an+1）的乘积, 即Sn=(1/4)*an+1 从而Sn-1=(1/4)*an 由an=Sn-Sn-1 =(1/4)*an+1-(1/4)*an 得(1/4)*an+1=an+(1/4)*an=(5/4)an 即an+1=5an 得(an+1):an=5 ∴已知正项数列{an}是 公比为5的等比数列.。
本文到此分享完毕，希望对大家有所帮助。
标签：
最新文章推荐
- 数列an的前n项和为sn,a1=1,an+1=2sn-前沿资讯
- 中国馆全称_中国馆地址、交通信息及相关介绍
- 海运开港时间查询_海运到港时间查询 快资讯
- 当前播报:厨房台面尺寸大约多宽
- 速读：里夫斯浓眉打出了怪物级的表现 里夫斯现在身体感觉比去年好很多最初不信新秀墙但它真实存在
- 独角兽高达_世界今日报
- 环球信息:盒子皮肤下线_盒子皮肤下线
- 事如春梦了无痕
- 世博大熊猫彩色金条价格今天多少一克（2023年03月08日）-新消息
- 世界热讯:道奇公羊2500皮卡报价_道奇公羊报价多少钱
X 关闭
资讯中心
兰州理工大学：深挖“战疫”育人新元素构建“大思政”格局
2022-05-20
新疆(含兵团)15日新增本土无症状感染者1例
2021-10-18
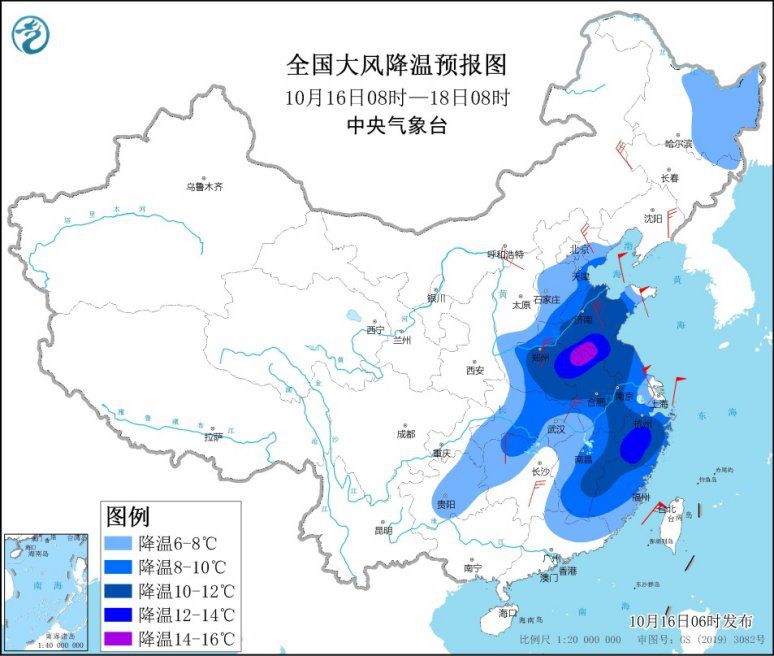强冷空气继续影响中东部地区 局地降温14℃以上
2021-10-18
中东部多地将迎立秋后最冷周末 雨雪天气持续
2021-10-18
X 关闭
热点资讯
-
1
杏花绽放催热“赏花经济” 吸引了大量游客前来旅游
-
2
上海籍阳性夫妻内蒙古密接、次密接者出现初筛阳性情况
-
3
内蒙古二连浩特：市民非必要不出小区、不出城
-
4
重庆一名潜逃24年的持枪抢劫嫌犯落网
-
5
销售有毒、有害食品 郭美美获刑二年六个月
-
6
陕西新增6名确诊病例1名无症状感染者 西安全面开展排查管控
-
7
《加强建设中国风湿免疫病慢病管理》倡议书：建立基层医院独立风湿科
-
8
游客因未购物遭导游辱骂？九寨沟：相关部门已介入调查
-
9
郭美美再入狱！销售有毒有害食品获刑2年6个月
-
10
2020年黄河青海流域冰川面积和储量较十年前缩减
-
11
5名“摸金校尉”落网 内蒙古警方破获一起盗掘古墓葬案